7강. 트리

by

학습개요

트리는 노드 혹은 정점으로 구성된 논리적인 계층이 있는 구조입니다. 데이터 사이의 계층 관계, 포함 관계 등을 나타내는 곳에서 사용되는 자료구조입니다. 나무를 거꾸로 놓은 모양이라 트리라 부릅니다. 그렇기 때문에 용어들도 나무와 관련 있게 뿌리, 잎, 서브 트리 등의 단어를 사용하며 정의됩니다. 트리에서는 용어들을 정확하게 아는 것이 중요합니다.

트리에 속한 모든 노드의 차수가 2 이하인 트리를 이진 트리라고 합니다. 이진 트리는 수학적으로 이론을 정리하기도 쉽고, 컴퓨터 내부에서 구현하기도 쉬워서 다양하게 자주 사용됩니다. 이진 트리에서 각 레벨이 허용되는 최대 개수 노드를 가질 때 그 트리를 가득 찬 이진 트리라고 합니다. 그리고 높이가 k인 이진 트리가 레벨 0부터 k-2까지 다 채우고 마지막 k-1 레벨에서 왼쪽부터 오른쪽으로 노드들이 차례로 채워졌을 때 완전 이진 트리라고 합니다.

트리의 각 노드를 모두 한 번씩 방문하는 것을 순회라고 합니다. 루트를 방문하는 순서에 따라 전위 순회, 중위 순회, 후위 순회라고 합니다. 트리를 순회한 방문 순서와 3장에서 학습한 수식의 전위, 중위, 후위 표기법이 같다는 것을 알 수 있습니다. 연관 지어서 학습하시면 더욱 좋으실 것 같습니다.

학습목표

  1. 트리의 용어와 표현 방법을 이해할 수 있다.
  2. 트리의 추상 자료형을 이해할 수 있다.
  3. 이진 트리의 개념과 구현 방법을 이해할 수 있다.
  4. 이진 트리의 순회 연산과 생성, 삽입, 삭제 연산을 이해할 수 있다.

연습문제

  1. 트리의 최상위 노드 혹은 부모가 없는 노드는 무엇인가?
    1. 자신노드
    2. 부모노드
    3. 잎노드
    4. 루트노드
      –
  2.  

    struct node *root ;
    void preorder(node *root) {
    if (root != NULL) {
    printf(“%c”, root → info) ;
    preorder(root → left) ;
    preorder(root → right) ;
    }  }

    지문의 프로그램이 수행하는 트리 순회는 무엇인가?
    1. 중위순회
    2. 후위순회
    3. 전위순회
    4. 역순회
    –

  3. 다음 중 완전 이진 트리는 무엇인가? 1

정리하기

  1. 트리는 논리적 계층이 있는 구조입니다.
  2. 트리를 구성하는 항목을 “노드(node)” 혹은 “정점(vertex)”이라고 합니다.
  3. 트리에서 루트는 부모를 갖지 않은 노드입니다.
  4. 트리에 있는 어떤 노드에 대해 그 노드로 들어오는 선의 개수를 진입 차수, 나가는 선의 개수를 진출 차수라 합니다.
  5. 트리에서 각 노드의 차수(degree of a node)는 진출 차수로 정의합니다.
  6. 트리의 차수(degree of a tree)는 트리 내의 각 노드의 차수 가운데 최대 차수로 정의합니다.
  7. 루트도 잎도 아닌 노드를 내부 노드라 하고 같은 부모를 갖는 노드들을 형제(sibling)라 합니다.
  8. 트리에서 각 노드의 레벨(level)은 루트로부터 그 노드까지 이어진 경로의 길이로 정합니다.
  9. 트리는 데이터의 계층 관계, 포함 관계 등을 나타내는 자료구조입니다.
  10. 트리에 속한 모든 노드의 차수가 2 이하인 트리를 이진 트리라고 합니다.
  11. 이진 트리에서 각 레벨이 허용되는 최대 개수 노드를 가질 때 그 트리를 가득 찬(perfect) 이진 트리라고 합니다.
  12. 높이가 k인 이진 트리가 레벨 0부터 k-2까지 다 채우고 마지막 k-1 레벨에서 왼쪽부터 오른쪽으로 노드들이 차례로 채워졌을 때 완전(complete) 이진 트리라고 합니다.
  13. 트리의 각 노드를 빠짐없이 한 번씩만 방문하는 것을 순회(traverse)라고 합니다.
  14. 루트를 방문하는 순서에 따라 각각 전위(preorder) 순회, 중위(inorder) 순회, 후위(postorder) 순회라고 구분하여 부릅니다.

트리의 순회방법

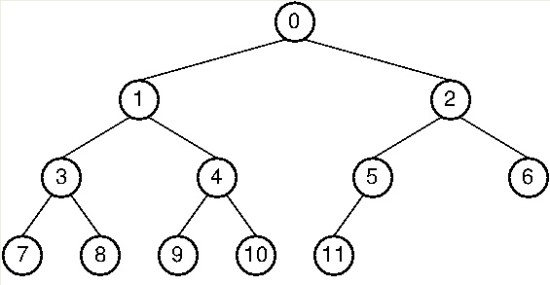
위와 같은 트리가 있다고 한다면 각각 순회방법은 다음과 같습니다.

  • 전위 순회 : 0->1->3->7->8->4->9->10->2->5->11->6
  • 중위 순회 : 7->3->8->1->9->4->10->0->11->5->2->6
  • 후위 순회 : 7->8->3->9->10->4->1->11->5->6->2->0
  • 층별 순회 : 0->1->2->3->4->5->6->7->8->9->10->11

★전위 순회는 뿌리->왼쪽 자식->오른쪽 자식 순
★중위 순회는 왼쪽자식-> 뿌리-> 오른쪽 자식
★후위 순회는 왼쪽자식->오른쪽 자식-> 뿌리
★층별 순회는 그냥 노드의 순서대로

Leave a Comment